728x90
Linear Regression (선형회귀) : 데이터들을 가장 잘 표현하는 직선의 방정식을 찾는 것
Data 를 대표하는 hypothesis를 직선의 방정식으로 설정
y = Ax + B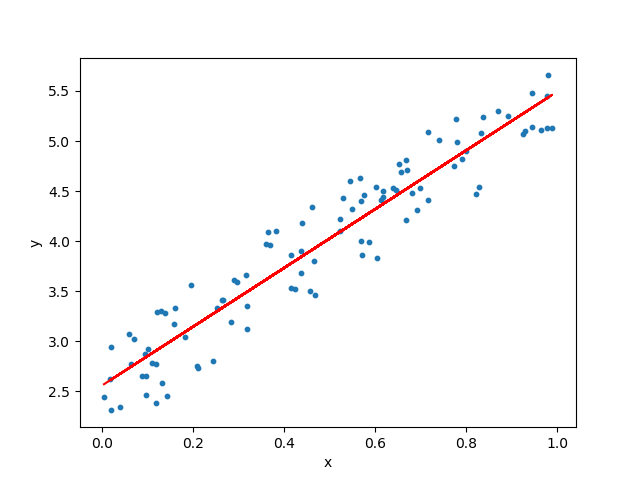
Step1) Hypothesis
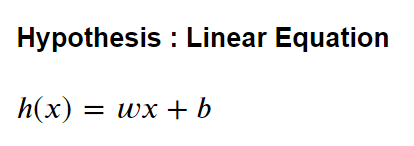
Step2) Cost function
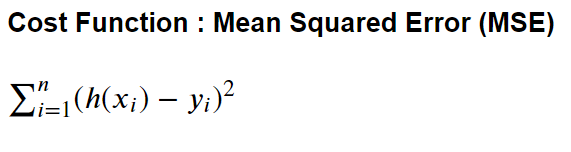
Step3) Training - gradient descent method
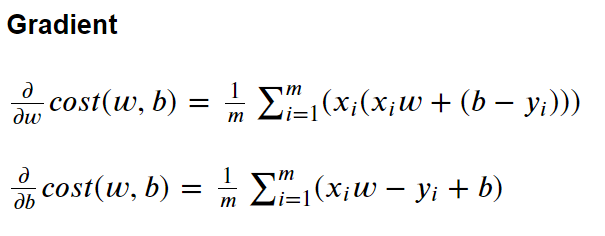

Numpy
w/o min-max scaling
#load module
import numpy as np
import matplotlib.pyplot as plt
#input & label (age and blood pressure)
x_input = np.array([15,20,25,30,31,35,42,43,45,50,55,56,66,67,68,70,71,73], dtype= np.float32)
labels = np.array([118,125,130,118,126,123,120,124,130,122,125,130,127,130,130,125.5,130,138], dtype= np.float32)
#weight and bias
W = np.random.normal()
B = np.random.normal()
#Function Generation
def Hypothesis(x) :
return W*x + B
def Cost() :
return np.mean((Hypothesis(x_input)- labels)**2)
def Gradient(x,y):
return np.mean(x*(W*x+(B-y))), np.mean((W*x-y+B))
def Predict(x):
return Hypothesis(x)
#Parameter
epochs = 100000
lr = 0.0005
training_idx = np.arange(0, epochs+1, 1)
cost_graph = np.zeros(epochs+1)
#Training
for cnt in range(0, epochs + 1):
cost_graph[cnt] = Cost()
if cnt%(epochs//20) == 0:
print("[{}] Cost = {}, W = {}, B = {}".format(cnt, Cost(), W,B))
grad_W, grad_B = Gradient(x_input, labels)
W -= lr * grad_W
B -= lr * grad_B
#Prediction
age = 29.0
print("{} years : {}mmHg".format(age, Predict(age)))
29.0 years : 123.037651955064mmHg
#Cost function graph
plt.title("'Cost / Epochs' Graph")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.plot(training_idx, cost_graph)
plt.xlim(0, epochs)
plt.grid(True)
plt.semilogy()
plt.show()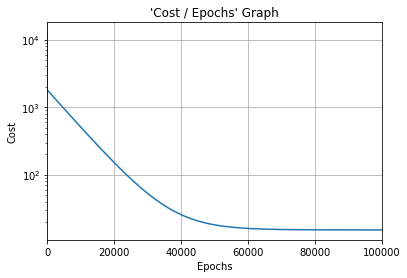
#labels and prediction graph
plt.title("Labels and Prediction Graph")
plt.xlabel("x input")
plt.ylabel("Labels and Prediction")
plt.scatter(x_input.reshape(-1,), labels.reshape(-1,),color = 'red', label='labels')
plt.plot(x_input.reshape(-1,), Hypothesis(x_input).reshape(-1,), label='predict')
plt.grid(True)
plt.legend(loc='upper left')
plt.show()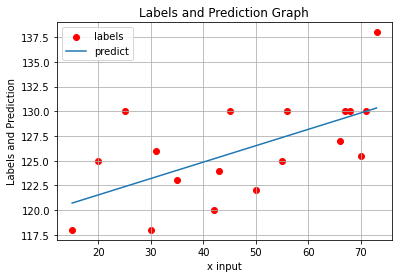
Tensorflow
w/ min-max scaling
#load module
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
#input & label (age and blood pressure)
x_input = tf.constant([15,20,25,30,31,35,42,43,45,50,55,56,66,67,68,70,71,73], dtype= tf.float32)
labels = tf.constant([118,125,130,118,126,123,120,124,130,122,125,130,127,130,130,125.5,130,138], dtype= tf.float32)
#weight and bias
W = tf.Variable(tf.random.normal(()), dtype = tf.float32)
B = tf.Variable(tf.random.normal(()), dtype = tf.float32)
#input min,max scaling
x_input_org = x_input
xmin, xmax = np.min(x_input), np.max(x_input)
x_input = (x_input-xmin)/(xmax-xmin)
#Function Generation
def Hypothesis(x) :
return tf.add(tf.multiply(x,W),B)
def Cost() :
return tf.reduce_mean(tf.square(Hypothesis(x_input)-labels))
def Predict(x):
return Hypothesis((x-xmin)/(xmax-xmin)).numpy()
#Parameter
epochs = 10000
lr = 0.01
opt = tf.keras.optimizers.SGD(learning_rate = lr)
training_idx = np.arange(0, epochs+1, 1)
cost_graph = np.zeros(epochs+1)
#Training
for cnt in range(0, epochs + 1):
cost_graph[cnt] = Cost()
if cnt%(epochs//20) == 0:
print("[{}] Cost = {}, W = {}, B = {}".format(cnt, Cost(), W.numpy(), B.numpy()))
opt.minimize(Cost, [W,B])
#Prediction
age = 29.0
print("{} years : {}mmHg".format(age, Predict(age)))
29.0 years : 123.12702178955078mmHg
#Cost function graph
plt.title("'Cost / Epochs' Graph")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.plot(training_idx, cost_graph)
plt.xlim(0, epochs)
plt.grid(True)
plt.semilogy()
plt.show()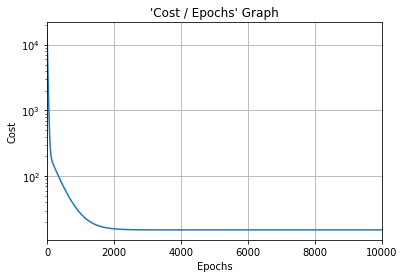
#labels and prediction graph
plt.title("Labels and Prediction Graph")
plt.xlabel("x input")
plt.ylabel("Labels and Prediction")
plt.scatter(x_input.numpy().reshape(-1,), labels.numpy().reshape(-1,),color = 'red', label='labels')
plt.plot(x_input.numpy().reshape(-1,), Hypothesis(x_input).numpy().reshape(-1,), label='predict')
plt.grid(True)
plt.legend(loc='upper left')
plt.show()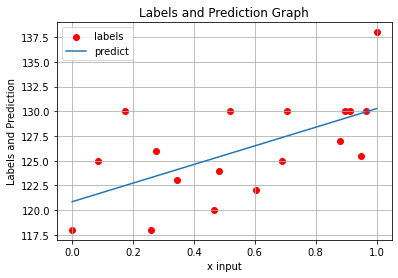
numpy)
age : 29
blood pressure : 123.037mmHg
tensorflow)
age : 29
blood pressure : 123.1270mmHg
| Numpy | Tensorflow | |
| 변수 | 일반 변수 선언 | training 할 변수는 tf.variable() 상수는 tf.constant() |
| 구현 | np.mean(), *, + | tf.reduce_mean() tf.square() |
| 학습 | 직접 구현 | optimizer, minimize 사용 |
728x90
'Machine Learning' 카테고리의 다른 글
| Supervised Learning - Logistic Regression (multi-variable 2) (0) | 2023.08.06 |
|---|---|
| Supervised Learning - Logistic Regression (multi-variable 1) (0) | 2023.08.05 |
| Supervised Learning - Linear Regression (multi-variable 2) (0) | 2023.08.05 |
| Supervised Learning - Linear Regression (multi-variable 1) (0) | 2023.08.05 |
| Machine Learning 개요 (0) | 2023.08.05 |



