728x90
Logistic Regression : 주어진 입력에 따라 discrete 한 값을 예측
(=Binary Classification)
Linear : H(x) ∈ (-inf, inf)
Logistic : H(x) ∈ [0,1]
Hypothesis function 으로 logistic function (sigmoid function) 적용하여 regression 진행
입력에 따라서 0~1 사이 값 출력
application) 메일의 스팸여부, 영화 감상 긍정/부정, 주식 종목 구분 등

Step1) Hypothesis

Step2) Cost function

Step3) Training - gradient descent method


Tensorflow
w/ min-max scaling
#load module
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
#input(age, BMI) & label(y/n)
x_input = tf.constant([[25,22],[25,26],[25,30],[35,22],[35,26],[35,30],[45,22],[45,26],
[45,30],[55,22],[55,26],[55,30],[65,22],[65,26],[65,30],[73,22],[73,26],[73,30]], dtype= tf.float32)
labels = tf.constant([[0],[0],[1],[0],[1],[0],[0],[0],[1],[0],[0],[1],[1],[1],[1],[0],[1],[1]], dtype= tf.float32)
#weight and bias
W = tf.Variable(tf.random.normal((2,1)), dtype = tf.float32)
B = tf.Variable(tf.random.normal((1, )), dtype = tf.float32)
#min-max scaling
x_input_org = x_input
xmin, xmax = np.min(x_input, axis = 0), np.max(x_input, axis = 0)
x_input = (x_input - xmin)/(xmax-xmin)
#Function Generation
def Hypothesis(x):
return tf.sigmoid(tf.add(tf.matmul(x,W),B))
def Cost():
return -tf.reduce_mean(labels * tf.math.log(Hypothesis(x_input)) + (1 - labels) * tf.math.log(1 - Hypothesis(x_input)))
def Predict(x):
return Hypothesis((x-xmin)/(xmax-xmin))
#Parameter
epochs = 10000
lr = 0.01
opt = tf.keras.optimizers.SGD(learning_rate = lr)
training_idx = np.arange(0, epochs+1, 1)
cost_graph = np.zeros(epochs+1)
check = np.array([0, epochs*0.01, epochs*0.08, epochs*0.2, epochs*0.4, epochs])
W_trained = []
B_trained = []
check_idx = 0
#Training
for cnt in range(0, epochs+1):
cost_graph[cnt] = Cost()
if cnt % (epochs//20) == 0:
print("[{:>6}] Cost = {:>10.4}, W = [{:>7.4} {:>7.4}], B = {:>7.4}".format(cnt, cost_graph[cnt], W[0,0], W[1,0], B[0]))
if check[check_idx] == cnt:
W_trained.append(W.numpy())
B_trained.append(B.numpy())
check_idx += 1
opt.minimize(Cost, [W,B])
#Prediction (using input value)
Hx = Hypothesis(x_input).numpy().reshape(-1,)
H = [int(h>0.5) for h in Hx] #0,1 class
for i in range(x_input.shape[0]):
print("Age : {:>7.4}, BMI : {:>7.4} , Label : {} => Class :{:>2}(Pred:{:>5.2})".format(x_input_org[i,0], x_input_org[i,1], labels[i], H[i], Hx[i]))
#Prediction (using new value)
test_set = tf.constant([[39.0, 26.0]], dtype = tf.float32)
Hx = Predict(test_set).numpy().reshape(-1,)
H = [int(h>0.5) for h in Hx] #0,1 class
test_set, Hx, H
print("Age : {:>7.4}, BMI : {:>7.4} => Class :{:>2}(Pred:{:>5.2})".format(test_set[0,0], test_set[0,1], H[0], Hx[0]))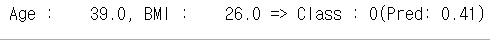
#Cost function graph
plt.title("'Cost / Epochs' Graph")
plt.xlabel("Epochs")
plt.ylabel("Cost")
plt.plot(training_idx, cost_graph)
plt.xlim(0, epochs)
plt.grid(True)
plt.semilogy()
plt.show()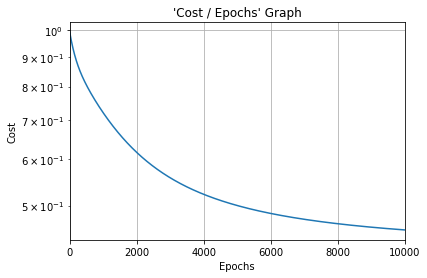
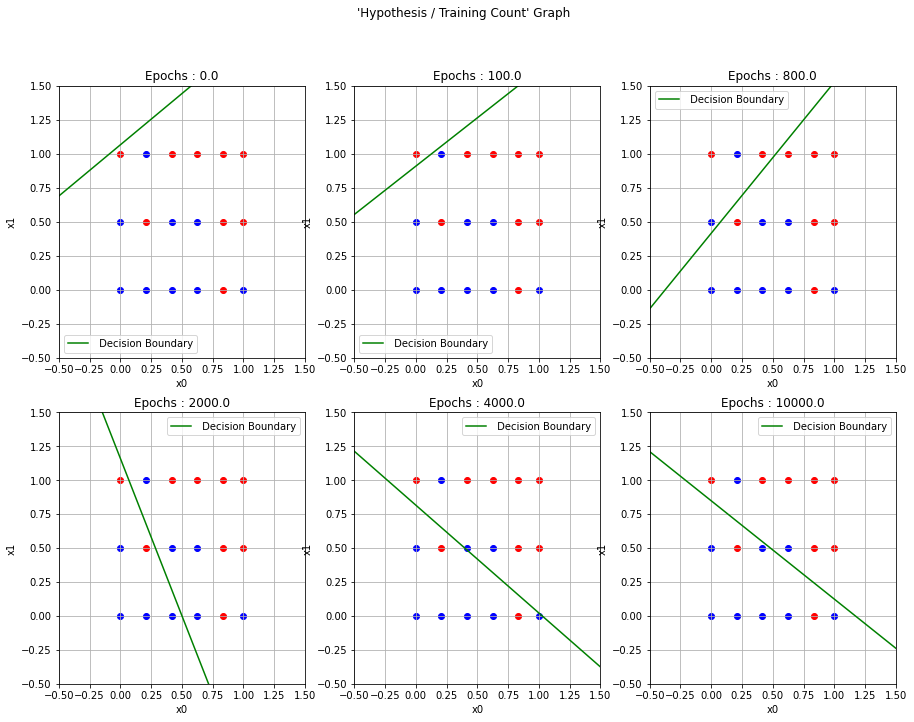
# 구분선 그리기
x_decision = np.linspace(-0.5, 1.5, 100)
fig, ax = plt.subplots(2, 3, figsize=(15, 11))
fig.suptitle("'Hypothesis / Training Count' Graph")
for ax_idx in range(check.size):
W = W_trained[ax_idx]
B = B_trained[ax_idx]
y_decision = -(W[0] * x_decision + B[0])/W[1]
# label의 값에 따라서 blue 또는 red 점 찍기
for i in range(labels.shape[0]):
if(labels[i][0] == 0):
ax[ax_idx // 3][ax_idx % 3].scatter(x_input[i][0], x_input[i][1], color='blue')
else:
ax[ax_idx // 3][ax_idx % 3].scatter(x_input[i][0], x_input[i][1], color='red')
ax[ax_idx // 3][ax_idx % 3].plot(x_decision, y_decision, label=' Decision Boundary', color='green')
ax[ax_idx // 3][ax_idx % 3].set_title("Epochs : {}".format(check[ax_idx]))
ax[ax_idx // 3][ax_idx % 3].set_xlim((-0.5, 1.5))
ax[ax_idx // 3][ax_idx % 3].set_ylim((-0.5, 1.5))
ax[ax_idx // 3][ax_idx % 3].set_xlabel("x0")
ax[ax_idx // 3][ax_idx % 3].set_ylabel("x1")
ax[ax_idx // 3][ax_idx % 3].grid(True)
ax[ax_idx // 3][ax_idx % 3].legend()
plt.show()
728x90
'Machine Learning' 카테고리의 다른 글
| Supervised Learning - Softmax Classfication (multi-variable 2) (0) | 2023.08.06 |
|---|---|
| Supervised Learning - Softmax Classification (multi-variable 1) (0) | 2023.08.06 |
| Supervised Learning - Logistic Regression (multi-variable 1) (0) | 2023.08.05 |
| Supervised Learning - Linear Regression (multi-variable 2) (0) | 2023.08.05 |
| Supervised Learning - Linear Regression (multi-variable 1) (0) | 2023.08.05 |



